APPROX-MIC Implementation Details¶
The core implementation of libmine is built from scratch in ANSI C starting from the pseudocode provided in DOI: 10.1126/science.1205438, Supplementary On-line Material (SOM), as no original Java source code is available. The level of detail of the pseudocode leaves a few ambiguities and in this section we list and comment the most crucial choices we adopted for the algorithm steps whenever no explicit description was provided. Obviously, our choices are not necessarily the same as in the original Java version (MINE.jar, http://www.exploredata.net/). The occurring differences can be ground for small numerical discrepancies as well as for difference in performance (DOI: 10.1093/bioinformatics/bts707).
In SOM, Algorithm 5, the characteristic matrix
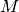 is computed in the
loop starting at line 7 for
is computed in the
loop starting at line 7 for 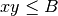 . This is in contrast with the
definition of the MINE measures (see SOM, Sec. 2) where the corresponding
bound is
. This is in contrast with the
definition of the MINE measures (see SOM, Sec. 2) where the corresponding
bound is 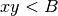 for all the four statistics. We adopted the same bound
as in the pseudocode, i.e.
for all the four statistics. We adopted the same bound
as in the pseudocode, i.e. 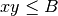 .
.The MINE statistic MCN is defined as follows in SOM, Sec. 2:
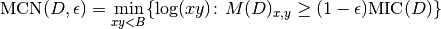
As for MINE.jar (inferred from Table S1), we set
 and
and
 to be in base 2. Finally, as specified in Point 1 above, we use
the bound
to be in base 2. Finally, as specified in Point 1 above, we use
the bound  as in the SOM pseudocode rather than the
as in the SOM pseudocode rather than the
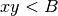 as in the definition. This led to implement the formula:
as in the definition. This led to implement the formula: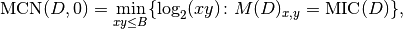
being
 the maximum value of the matrix
the maximum value of the matrix  .
.In EquipartitionYAxis() (SOM, Algorithm 3, lines 4 and 10), two ratios are assigned to the variable desiredRowSize, namely
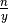 and
and
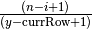 . We choose to consider the
ratios as real numbers; a possible alternative is to cast desiredRowSize to
an integer. The two alternatives can give rise to different
. We choose to consider the
ratios as real numbers; a possible alternative is to cast desiredRowSize to
an integer. The two alternatives can give rise to different 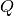 maps,
and thus to slightly different numerical values of the MINE statistics.
maps,
and thus to slightly different numerical values of the MINE statistics.In some cases, the function EquipartitionYAxis() can return a map
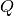 whose number of clumps
whose number of clumps 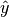 is smaller than
is smaller than 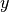 , e.g. when
in
, e.g. when
in 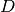 there are enough points whose second coordinates coincide. This
can lead to underestimate the normalized mutual information matrix
there are enough points whose second coordinates coincide. This
can lead to underestimate the normalized mutual information matrix
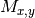 (SOM, Algorithm 5, line 9), where
(SOM, Algorithm 5, line 9), where 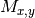 is obtained
by dividing the mutual information
is obtained
by dividing the mutual information 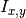 for
for
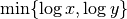 . To prevent this issue, we normalize instead
by the factor
. To prevent this issue, we normalize instead
by the factor 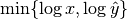 .
.The function GetClumpsPartition(
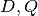 ) is discussed (SOM page 12), but
its pseudocode is not explicitely available. Our implementation is defined
here in GetClumpsPartition() algorithm. The function returns the map
) is discussed (SOM page 12), but
its pseudocode is not explicitely available. Our implementation is defined
here in GetClumpsPartition() algorithm. The function returns the map 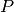 defining the clumps for the set
defining the clumps for the set 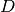 , with the constraint of keeping in
the same clump points with the same
, with the constraint of keeping in
the same clump points with the same 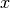 -value.
-value.
GetClumpsPartition() algorithm
We also explicitly provide the pseudocode for the GetSuperclumpsPartition() function (SOM page 13) in GetSuperclumpsPartition() algorithm. This function limits the number of clumps when their number k is larger than a given bound
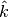 . The function calls the GetClumpsPartition() and, for
math:k>hat{k} it builds an auxiliary set
. The function calls the GetClumpsPartition() and, for
math:k>hat{k} it builds an auxiliary set 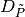 as an input
for the EquipartitionYAxis function discussed above (Points 3-4).
as an input
for the EquipartitionYAxis function discussed above (Points 3-4).
GetSuperclumpsPartition() algorithm
We observed that the GetSuperclumpsPartition() implemented in MINE.jar may fail to respect the
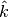 constraints on the maximum number of clumps and a
map
constraints on the maximum number of clumps and a
map 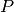 with
with 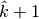 superclumps is actually returned. As an
example, the MINE.jar applied in debug mode (d=4 option) with the same
parameters (
superclumps is actually returned. As an
example, the MINE.jar applied in debug mode (d=4 option) with the same
parameters (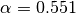 ,
, 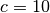 ) used in the original work to the
pair of variables (OTU4435,OTU4496) of the Microbioma dataset, returns
) used in the original work to the
pair of variables (OTU4435,OTU4496) of the Microbioma dataset, returns
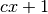 clumps, instead of stopping at the bound
clumps, instead of stopping at the bound 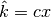 for
for
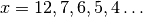 .
.The possibly different implementations of the GetSuperclumpsPartition() function described in Points 6-7 can lead to minor numerical differences in the MIC statistics. To confirm this effect, we verified that by reducing the number of calls to the GetSuperclumpsPartition() algorithm, we can also decrease the difference between MIC computed by minepy and by MINE.jar, and they asymptotically converge to the same value.
In our implementation, we use double-precision floating-point numbers (
doublein C) in the computation of entropy and mutual information values. The internal implementation of the same quantities in MINE.jar is unknown.In order to speed up the computation of the MINE statistics, we introduced two improvements (with respect to the pseudo-code), in OptimizeXAxis(), defined in Algorithm 2 in SOM):
- Given a
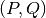 grid, we precalculate the matrix of
number of samples in each cell of the grid, to speed up the
computation of entropy values
grid, we precalculate the matrix of
number of samples in each cell of the grid, to speed up the
computation of entropy values 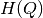 ,
, 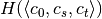 ,
, 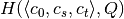 and
and 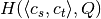 .
. - We precalculate the entropy matrix
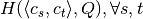 to speed up the computation of
to speed up the computation of
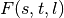 (see Algorithm 2, lines 10–17 in SOM).
(see Algorithm 2, lines 10–17 in SOM).
These improvements do not affect the final results of mutual information matrix and of MINE statistics.
- Given a